
Na teoria dos números, A função totiente de Euler, conta o número de inteiros positivos menores que m e relativamente primos a m. Para um número primo p, φ(p)=p-1.
Pode ser definido mais formalmente como o número de inteiros k no intervalo 1 ≤ k ≤ n para o qual o maior divisor comum mdc(n, k) é igual a 1.
O que é o pequeno teorema de Fermat
Pequeno teorema de Fermat diz que se p é primo e a não é um múltiplo de p, então
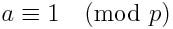
A generalização de Euler do pequeno teorema de Fermat diz que se a um primo relativo para m, então
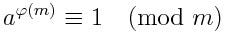
A função totiente de Euler é multiplicativa, isto é, se a e b são entre si, então φ(ab) = φ(a)φ(b). Nós usaremos esse fato em outras discussões
A prova de generalização
Seja r=φ(n) e b₀, b₁, …, bᵣ, números inteiros, primos ente si dois a dois, e todos primos com n. Então ab₀, ab₁, …, abᵣ, ainda será congruente (mod n), para i=1,2,…r.
Os conjuntos b₀, b₁, …, bᵣ e ab₀, ab₁, …, abᵣ são iguais (mod n). Então multiplicando tudo
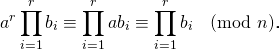
Então,
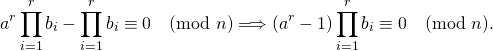
Assim temos que, (aʳ-1) ≡ 0 (mod n) e como aʳ ≡ 1 (mod n) e r = φ(n), então
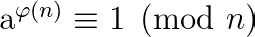
Teste de primalidade
Uma das melhores coisas sobre esse teorema é o teste da primalidade.
O contrapositivo do pequeno teorema de Fermat é útil: se a congruência aᵖ⁻¹ ≡ 1 (mod p) não é verdadeiro, então p é não primo ou a é um múltiplo de p. Na prática, a é muito menor que p, e assim pode-se conclua que p não é primo.
Tecnicamente, este é um teste para não primalidade: só pode provar que um número é não primo. Por exemplo, se 2ᵖ⁻¹ ≢ 1 (mod p), então sabemos que p não é primo. Mas se 2ᵖ⁻¹ ≡ 1 (mod p ) então sabemos que o teste não falhou; mas não temos certeza se p é primo ou não. Então, nós tentamos outro valor de a, por exemplo 5, e testamos se 5ᵖ⁻¹ ≡ 1 (mod p).
Em teoria parece perfeito, então toda a teoria da criptografia foi arruinada? Claro que não, porque mesmo fácil de entender, mas olhando em termos computacionais, isto é problemático, por exemplo, para um pequeno número como 223, e para a com valor de 2, nós temos;

Sabemos que 223 é primo, mas 2²²³ é difícil de calcular mesmo em robustos computadores, então números como 2321412341243123423413263466567678352323 é mais difícil determinar, mas toda a teoria é útil, com muitas implicações na criptografia e teoria dos números. Eu vou discutir isso em outros posts.