
É muito mais fácil e rápido multiplicar números do que fatorá-los. Isso é o fundamento da criptografia RSA.
Em particular, a criptografia RSA funciona com dois primos grandes p e q, pois é rápido e fácil encontrar o produto pq, mas é difícil recuperar o fatores p e q do produto n. Geralmente p e q são números com centenas de números, e fatorar um número desta magnitude é muito lento.
O algoritmo
Para codificar a mensagem, precisamos de n = pq e um inteiro positivo e que deve ser reversível módulo φ(n). Nós conversamos sobre a função de trabalho de Euler antes.
Vamos chamar o par de chaves de codificação (n, e) do sistema RSA. Vamos codificar cada bloco de mensagens separadamente e a mensagem final será a sequencia de blocos.
Importante: Blocos já codificados não podem ser montados para formar um novo número. Isso deve tornar a decodificação impossível, como veremos mais adiante!
Vamos agora mostrar como codificar cada bloco b. Vamos chamar o bloco codificado de C(b). Primeiro, lembre-se de que b é um número inteiro menor que n. Nós calculamos C(b) como segue:
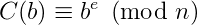
onde 0≤C(b)<n.
Vamos ver como decodificar um bloco da mensagem codificada. A informação que precisamos decodificar consiste em dois números: n e o inverso de e módulo φ(n), que denotamos d. Vamos chamar o par (n, d) da chave de decodificação . Seja o único bloco da mensagem codificada. Então D(a) será o resultado do processo de decodificação. A maneira de calcular D(a) é:
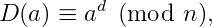
onde 0 ≤ D (a) <n.
Primeiro, é muito fácil calcular d, se tivermos φ(n) e e: simplesmente aplique o algoritmo Euclideano estendido. Por outro lado, é claro que se b é um bloco da mensagem original, então esperamos D(C(b)) = b, caso contrário teremos um código inútil.
Finalmente, insistimos em codificar usando n e decodificar usando p e q; então você precisa fatorar n para decodificar. Neste ponto nós vemos que isso não é estritamente verdadeiro. Além de n em si, precisamos conhecer o inverso d de e modulo φ(n) para decodificar. Acontece que nós apenas sabemos calcular d aplicando o algoritmo estendido a e e φ(n). O que seria equivalente a fatorá-lo.
Prova de que o RSA funciona
A pergunta óbvia que agora surge é: D(C(b)) = b? Isso é, decodificando um bloco de mensagem codificada, podemos encontrar um bloco da mensagem original? Se isso não for verdade todo o nosso esforço não tem significado…
Considere n = pq. Provaremos que D(C(b)) ≡ b mod (n), com 1 ≤ b, D(C(b)) ≤ n-1.
Por definição, nós temos:
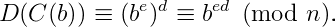
Mas como d é o inverso de e módulo φ(n). Então existe um inteiro k tal que ed = 1 + kφ (n). Logo,
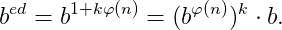
Se b e n são primos entre si, então podemos usar o Teorema de Euler:
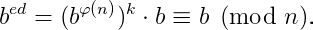
Suponha agora que b e n não sejam primos entre si. Desde que n = pq, com p e q primos distintos, temos φ(n) = (p-1)(q-1).
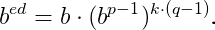
Se b e p são primos entre si, então podemos usar o Teorema de Fermat, e temos bᵖ⁻¹ ≡ 1 mod (p). Portanto, bᵉᵈ ≡ b mod (p), qualquer que seja b. Fazendo o mesmo para o primo q, obtemos, bᵉᵈ ≡ b mod (q). Portanto,
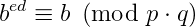
como queríamos.
Implementação
Como desenvolvedor, eu tenho que colocar código em todos os lugares, mesmo quando não tem necessidade, mas vou colocar aqui uma simples implementação deste algoritmo, e que pode ser útil depois.
#!/usr/bin/python2
import sys, ast
from optparse import OptionParser
parser = OptionParser("usage: %prog [options]")
parser.add_option("-p", "--p", dest="p", action="store", default='223', help="Value of p prime")
parser.add_option("-q", "--q", dest="q", action="store",default='59', help="Value of q prime")
parser.add_option("-e", "--encrypt", dest="encrypt", action="store_true",default=False, help="Do operation encrypt")
parser.add_option("-d", "--decrypt", dest="decrypt", action="store_true",default=False, help="Do operation decrypt")
parser.add_option("-m", "--message", dest="message", action="store",default=None, help="Message for encrypted/decrypted")
parser.add_option("-k", "--key", dest="e", action="store",default='97', help="Number e, for prime relative with phi")
(options, args) = parser.parse_args()
def gcd(a, b):
while b != 0:
a, b = b, a % b
return a
def multiplicative_inverse(e, phi):
d = 0
x1 = 0
x2 = 1
y1 = 1
temp_phi = phi
while e > 0:
temp1 = temp_phi/e
temp2 = temp_phi - temp1 * e
temp_phi = e
e = temp2
x = x2- temp1* x1
y = d - temp1 * y1
x2 = x1
x1 = x
d = y1
y1 = y
if temp_phi == 1:
return d + phi
def is_prime(num):
if num == 2:
return True
if num < 2 or num % 2 == 0:
return False
for n in xrange(3, int(num**0.5)+2, 2):
if num % n == 0:
return False
return True
def generate_keypair(p, q, e):
if not (is_prime(p) and is_prime(q)):
raise ValueError('Both numbers must be prime.')
elif p == q:
raise ValueError('p and q cannot be equal')
n = p * q
phi = (p-1) * (q-1)
if gcd(e, phi) != 1:
raise ValueError('e must be relative prime with phi')
d = multiplicative_inverse(e, phi)
return ((e, n), (d, n))
def encrypt(pk, plaintext):
key, n = pk
cipher = [(ord(char) ** key) % n for char in plaintext]
return cipher
def decrypt(pk, ciphertext):
key, n = pk
try:
plain = [chr(((char ** key) % n)) for char in ciphertext]
except ValueError as error:
print("It's not possible decrypt this text with those numbers p, q and e!")
exit(0)
return ''.join(plain)
if __name__ == '__main__':
encrypted_msg=None
print ("RSA Encrypter/ Decrypter")
print ("Generating your public/private keypairs now . . .")
public, private = generate_keypair(int(options.p), int(options.q), int(options.e))
print ("Your public key is ", public ," and your private key is ", private)
if(options.encrypt):
if (options.message is None):
message = raw_input("Enter a message to encrypt with your private key: ")
else:
message = options.message
encrypted_msg = encrypt(private, message)
print ("Your encrypted message is: ")
print (encrypted_msg)
if(options.decrypt):
if (encrypted_msg is None):
if(options.message is None):
text=raw_input("Enter a message to decrypt with your private key: ")
encrypted_msg = ast.literal_eval(text)
else:
encrypted_msg = ast.literal_eval(options.message)
print ("Decrypting message with public key ", public ," . . .")
print ("Your message is:")
print (decrypt(public, encrypted_msg))
O código no github está aqui